Successful mathematical problem solving involves insight, strategy and decision making, but also is improved through experience within many different tasks.
Here are a few problems that we have been considering in Hertfordshire; in lessons or in problem-solving events:
Year 9 or 10
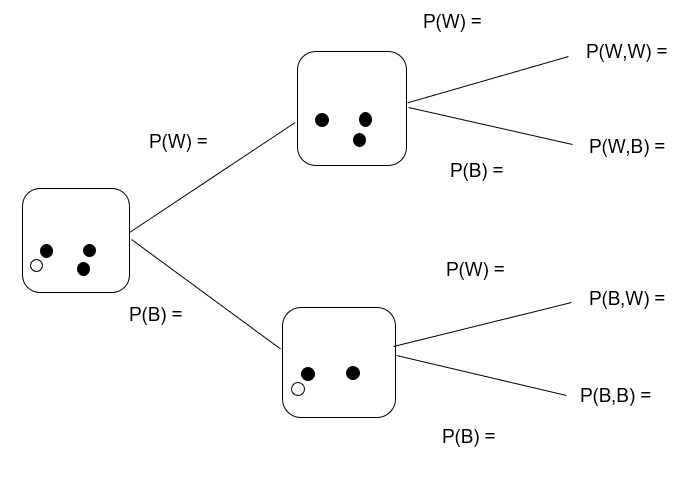
Suppose we would like to put some black and white beads in a bag so that the probability of picking 2 beads of the same colour without replacement is equal to
. One solution is 1 white and 3 black beads. Can you show that this works and find other possibilities?
Hint: The answers are all drawn from a standard set of numbers.
Year 10 or 11
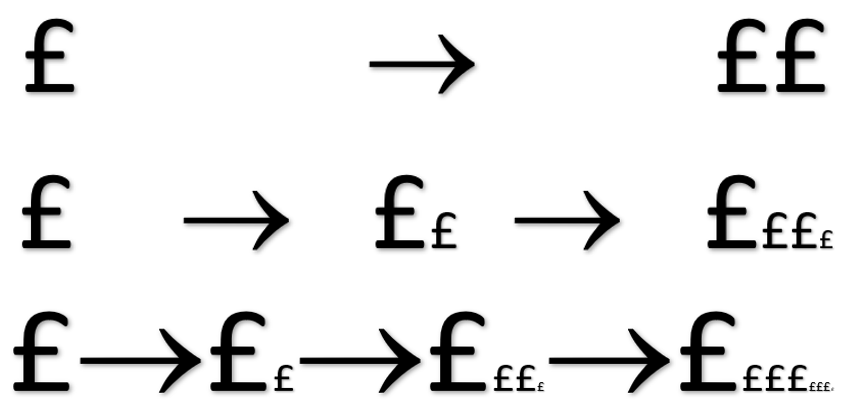
How much difference does it make to the answer to a compound interest problem if I wish to find my total final amount when I increase by 100% once, or by 50% twice, or by 33% three times, or by 25% four times, … , or by 10% ten times, … , or by 5% twenty times, … , or by 1% one hundred times etc? Is there a pattern or trend? How does the diagram relate to the problem?
Hint: Jacob Bernoulli discovered that the answers tend to a limiting value.
Year 12 or 13
Consider a polynomial . What could graphs of the form maths equation look like?
Eg If maths then consider the graph maths equation which gives two straight lines maths and maths. The diagram below uses maths equation
Hint: Polynomials with turning points will give more interesting answers.

Problem solving events
Discover problem solving events for your students in the East of England: