Today’s classroom use of algebra tiles is not breaking new ground. Almost four thousand years ago, the Ancient Babylonians used similar tiles to solve quadratic equations by completing the square. Algebraic notation was not even heard of in Babylonian times. Instead, they used a geometric process, using area to solve quadratic equations.
Let’s have a look at the following equation,
\(x^{2}+10x=24\)
Ancient Babylonians would have represented this equation using a square of length \(x\) and a rectangle of width \(x\) and length \(10\), the area of which would be \(24\). (we should label this picture 1) They could create a square by moving half of the rectangle [that is \(5x\)] to create a (loose) L shape. (we should label the second, picture 2). Similarly, I could represent this using algebra tiles.
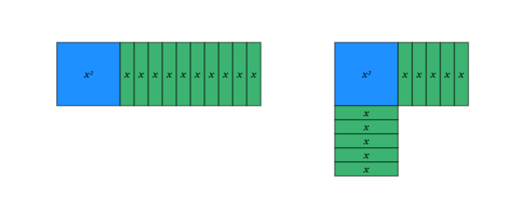
If I (or the Babylonian mathematicians) fill in the gap, the area wouldn’t be \(24\) anymore; it would be \(24 + 25\), so \(49\). And this will look like this (the completed square)
Remember, \(24=x^{2}+10x\) and \(25\) is represented with the \(25\) individual yellow tiles. (see the picture below)
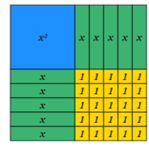
Algebra tiles can be used to solve equations, collect like terms, solve quadratics, complete the square, factorise, and expand brackets, to name but a few. Double-sided tiles and zero pairs can also start to make more sense of negative numbers. This helps pupils to cope with the abstract. This hands-on approach was good enough for the Babylonians; surely it is strong enough for us to make sense of some very abstract or procedural maths.
If you are interested in professional development on Higher GCSE topics or post 16 maths either for yourself or your department, please contact your Local Area Coordinator.
For online manipulatives, I used MathsBot.
by Steven Ladley