Sometimes in maths, little quirky facts can add to the richness and enjoyment of the subject as well as challenge and provoke investigation and discussion. I have a lovely little “fact” to share with you today, with a challenge to show why it is true, given a few reasonable assumptions and approximations.
Suppose you were to lie face-down on the ground, so that you form one short side of a rectangle, with the other short side being directly opposite you on the other side of the earth (see diagram below). I claim that area of this rectangle is equal to that of a square whose side is the distance from your eyes to the horizon when you are standing up.
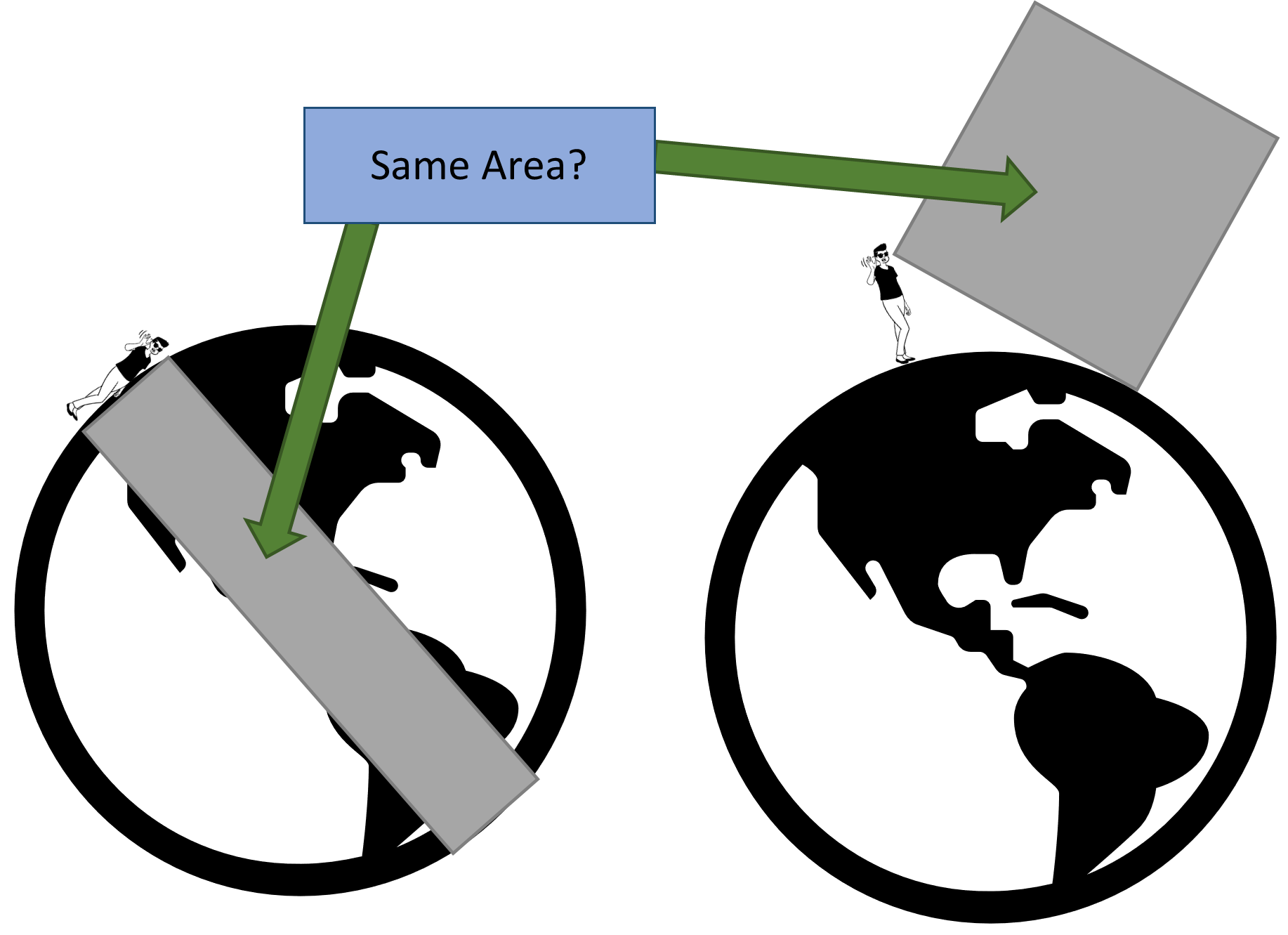
Some questions that this might raise are:
- What physical assumptions might have been made?
- What mathematical approximations might have been made?
- Can we use this to estimate the distance to the horizon for someone standing by the seashore?
- Is the distance to the horizon is proportional to the square root of your height? What other questions does this allow us to answer?
I would encourage you to consider these questions yourself and see if you can obtain the same result as me, before reading further.
Some assumptions and approximations that I made were:
- The earth is smooth and spherical.
- Your eyes are right at the top of your body.
- The radius of the earth is much, much larger than your height.
Giving names to things:
- The person’s height is \(h\)
- The radius of the earth is \(r\)
- The distance to the horizon is \(x\)
Consider the following diagram:

Applying Pythagoras:
\(r^{2} + x^{2}\) = \(r+h^{2}\)
\(⟹ r^{2} + x^{2} = r^{2}+2rh + h^{2}\)
\(⟹x^{2} = 2rh + h^{2}\)
\(\approx 2rh\)
Is this final approximation reasonable? Considering \(h^{2}\) as a percentage of \(2rh\) may help answer this!
Note that the diameter of the earth is \(2r\) and so \(2rh\) is the area of the rectangle formed by the person lying down in the original diagram, while \(x^{2}\) is the area of the square whose side is the distance from their eyes to the horizon when standing up!
Our most useful result is that the distance to the horizon is \(\sqrt{2rh}\). You might know that the diameter of the earth is about 8 000 miles. You might also know that successive Fibonacci numbers give conversion ratios between miles and kilometers (oh, you didn’t?, well have that for free!) so that’s about 13 000 km or 13 000 000 m. A typical person is a little under 2 m tall, so let’s say \(r2\times h\) is about 25 000 000 m2, which is conveniently a square number, whose root is 5 000 m, or (using Fibonacci again) about 3 miles.
Knowing that the distance to the horizon is proportional to the square root of your height means that you could, for example, deduce that if you were 100 times taller (or, more realistically, standing at the top of a 200 m skyscraper), then you could only see 10 times further, so about 30 miles.
It is probably worth noting here that we are only considering the distance to the horizon. Objects (people, buildings, mountains) that are located beyond this distance may well be visible if they rise above it. As an extension exercise, you might want to consider how far apart two objects, of different heights, need to be before they are completely hidden from each other by the horizon!